來到Day5，相信大家都對zk-SNARK有一定的了解，知道它有什麼用途和價值，今天就進一步講解zk-SNARK的核心原理和重點。
同時也預告一下，往後的文章會涉及到一些數學公式，所以要有心理準備，如果有什麼不明白，都可以隨時留言發問問題。

今天就講解一下zk-SNARK - quadratic arithmetic program (QAP)

zk-SNARK的QAP轉換

首先，zk-SNARKs不能直接應用於任何運算問題，所以必須要思考怎樣可以以正確的形式來解決這個運算問題。
這種正確的形式是二次算術程式(quadratic arithmetic program - QAP)，它可以將函數程式碼轉換為QAP。

接著會以例子說明:
要證明你是知道三次方程式的解：x**3 + x + 5 == 35(在這裡的答案是3)。
由於這個例子所產生的 QAP 不會很大，可以透過例子看到相關機制的原理及運作情況，以此作為例子解釋應該會比較好。

根據例子，得出函數如下：

def qeval(x):
    y = x**3
    return x + y + 5

• Flattening
  第一步是「Flattening」過程，將可能包含任意複雜語句和表達式的原始程式碼轉換為具有兩種形式的語句序列:

  • 第一種形式:

  x = y 
  

  其中 y 可以是變數或數字，

  • 第二種形式:

  x = y (op) z 
  

  其中 op 可以是加、減、乘、除，y 和 z 可以是變數、數字或其本身的子表達式。

可以將語句中的每一個視為電路中的邏輯閘(logic gates)。
上述程式碼進行Flattening處理後如下:

sym_1 = x * x
y = sym_1 * x
sym_2 = y + x
~out = sym_2 + 5

• Gates to R1CS
  將其轉換為 rank-1 constraint system (R1CS) 的系統。
  R1CS 是由三個向量 (a、b、c) 組成的一群序列，R1CS 的解向量 s，其中 s 必須滿足方程式 sa * sb - sc = 0，
  如下圖所示的R1CS:
  

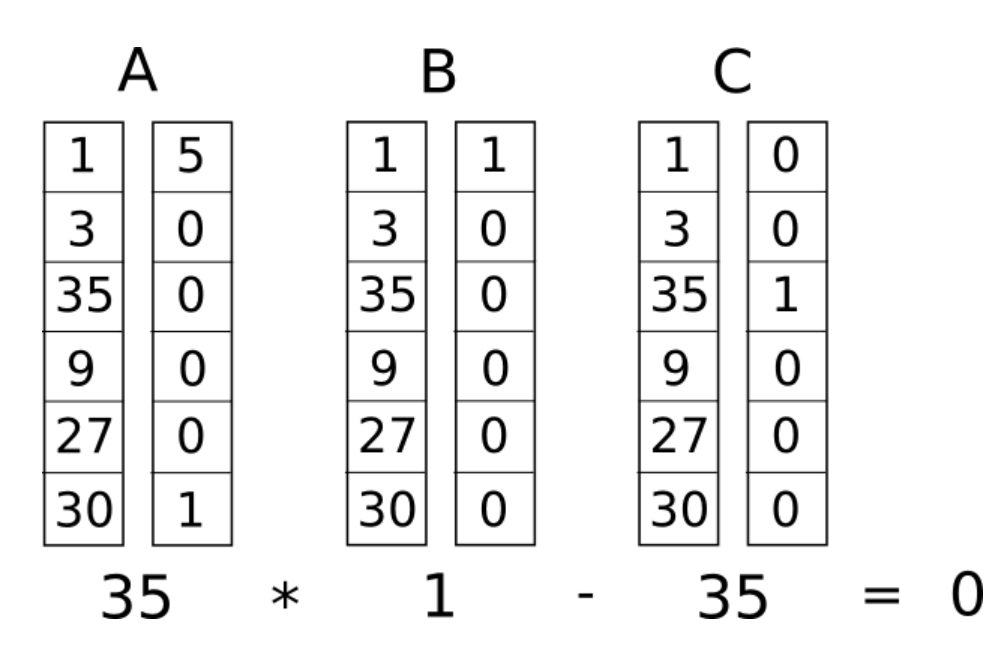
但在真實應用有機會設計各種約束，每個邏輯閘(logic gate)其實都表示一個約束。
利用數學方式，會有一種標準方法可以將邏輯閘轉換為 (a, b, c) 三個向量 。
每個向量的長度等於系統中變數的總數，包括代表數字1的第一個索引處的虛擬變數~one、輸入變數、代表輸出的虛擬變數~out，然後是所有的向量，sym1和sym2）。

首先，會進行變數映射(variable mapping):

'~one', 'x', '~out', 'sym_1', 'y', 'sym_2'

解向量將按順序包含所有這些變數的分配。
現在進入第一道門(sym_1 = x * x):

a = [0, 1, 0, 0, 0, 0]
b = [0, 1, 0, 0, 0, 0]
c = [0, 0, 0, 1, 0, 0]

可以留意到，如果解向量在第二個位置會包含3，在第四個位置會包含9，那麼無論解向量的其餘內容如何，算術檢查的結果為 3 * 3 = 9，並且所以它會過去的。如果解向量第二個位置為-3，第四個位置為9，則檢查也會通過，因為算術檢查的結果為 -3 * -3 = 9。
如果解向量在第二個位置有 7，在第四個位置有 49，算術檢查的結果為 7 * 7 = 49。因此檢查會通過順利通過第一次檢查的要求:其實只是驗證第一個閘的輸入和輸出的一致性，只要滿足R1CS 的解向量s就可以。

現在進入第二道門(y = sym_1 * x):

a = [0, 0, 0, 1, 0, 0]
b = [0, 1, 0, 0, 0, 0]
c = [0, 0, 0, 0, 1, 0]

其實跟第一個算術檢查相似，在這裡會以檢查是否滿足公式 sym_1 * x = y。

現在進入第三道門(sym_2 = y + x):

a = [0, 1, 0, 0, 1, 0]
b = [1, 0, 0, 0, 0, 0]
c = [0, 0, 0, 0, 0, 1]

這裡的模式有些不同: 它將解向量中的第一個元素乘以第二個元素，然後乘以第五個元素，將兩個結果相加，並檢查總和是否等於第六個元素。由於解向量中的第一個元素始終為 1，因此這只是一個加法檢查，檢查輸出是否等於兩個輸入的總和。

現在進入第四道門(~out = sym_2 + 5):

a = [5, 0, 0, 0, 0, 1]
b = [1, 0, 0, 0, 0, 0]
c = [0, 0, 1, 0, 0, 0]

點積檢查的工作原理是取解向量中的第六個元素，然後加入第一個元素的五倍數值(所以如果第一個元素是1，就表示是 1 * 5 = 5)，接著再對照第三個元素進行檢查。

在這個例子，R1CS只有四個限制條件。而見證人只是對所有變數的賦值包括輸入、輸出和內部變數，如下:

[1, 3, 35, 9, 27, 30]

透過Flattening，從輸入變數賦值 x=3 開始，然後基於預設變數及限制條件作出相關運算驗證。
將係數向量依順序排列，可以得到A, B, C三矩陣，從而得出完整的 R1CS:

A
[0, 1, 0, 0, 0, 0]
[0, 0, 0, 1, 0, 0]
[0, 1, 0, 0, 1, 0]
[5, 0, 0, 0, 0, 1]
B
[0, 1, 0, 0, 0, 0]
[0, 1, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 0]
C
[0, 0, 0, 1, 0, 0]
[0, 0, 0, 0, 1, 0]
[0, 0, 0, 0, 0, 1]
[0, 0, 1, 0, 0, 0]

• RICS to QAP
  下一步是利用 R1CS 及將其轉換為 QAP 形式，轉換之後會使用多項式而不是點積形式，它能夠實現完全相同的邏輯。接下來可以按照以下方式來進行相關轉換動作。首先從四組三個長度為 6 的向量(四道門)變成六組三個三階多項式，其中在每個 x 座標處評估多項式(可以理解為它是代表一個約束)。換言之，計算 x=1 處的多項式時，可以得到第一組向量，如果計算 x=2 處的多項式時，就可以得到第二組向量，如此類推。

然而這個換轉可以使用拉格朗日插值法來進行。將會在之後的教學中進行詳細講解，敬請期待。

先舉個一個例子以說明，假設我們想要一個通過 (1, 3)、(2, 2) 和 (3, 4) 的多項式。我們就必須先建立一個能夠通過 (1, 3)、(2, 0) 和 (3, 0) 的多項式。

(x - 2) * (x - 3)

在 X = 1 的位置進行一些調整

(x - 2) * (x - 3) * 3 / ((1 - 2) * (1 - 3))

可以得出:

1.5 * x**2 - 7.5 * x + 9

然後繼續對其他兩點做同樣的動作。

上述演算法需要 O(n**3) 的時間，因為有 n 個點，每個點需要 O(n**2) 時間將多項式相乘，但可以減少到 O(n**2) 時間，使用 fast Fourier transform algorithms等演算法可以進一步減少運算時間，在zk-SNARK中，通常情況都會有數千道門，如果能減少每道門的運算時間，最後就可以節省很多時間，會有明顯的效率提升。